I needed a way to test if a background color is light or dark in order to choose an appropriate text color (black on light colors and white on dark colors), you can find yourself in the same problem if you try to convert an image to grayscale.
I found many approaches that didn’t work well, I’ll describe them and the problems I discovered below – but first – the successful solution.
I finally found a solution that actually works on this web page the formula is:
brightness = sqrt( .241 R2 + .691 G2 + .068 B2 )
Or, in C# using the WPF's Color structure System.Windows.Media.Color (the same exact code should also work with the System.Drawing.Color structure used in WinForms and WebForms):
private static int Brightness(Color c)
{
return (int)Math.Sqrt(
c.R * c.R * .241 +
c.G * c.G * .691 +
c.B * c.B * .068);
}
This method will return a number in the rage of 0 (black) to 255 (White) and to set the foreground color based on the Brightness method:
Color textColor = Brightness(backgroundColor) < 130 ? Colors.White : Colors.Black;
I selected cutoff value of 130 by trial and error and it reflects my taste, every value in the rage 128-145 will give acceptable results.
Here is a table of all the named colors in .net 3.0, each with its name in readable text on it based on the code above, the number in parenthesis is the brightness – click on the image to view it in full size (in a new browser window).
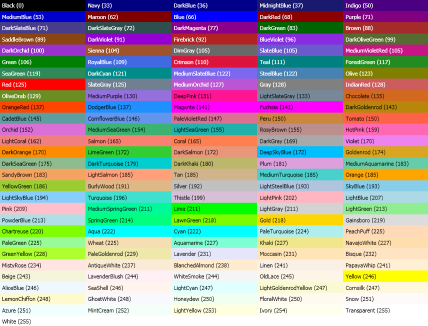
Usually, when talking about color theory the range 0-1 is used for each component – so (0,0,0) is black, (1,1,1) is white and (0.5,0.5,0.5) is 50% gray, I’m not using this range, I’m using the 0-255 range used in most programming environments.
Why Not HSL or HSV?
You may think that the luminance (or lightness) component of the HSL color system or the value component of HSV will solve this problem, I did, but I was wrong.
The L component of the HSL and the V component of HSV describe the brightness of a color relative to a base color, if this base color is blue you will get a darker color than if this base color is yellow, HSL and HSV are very useful if you need to create a lighter or darker version of a color but aren’t very useful if you want to know how bright a color is.
The Naïve RGB Algorithm
If RGB 0,0,0 is black and RGB 255,255,255 is white then R+B+G should give us a good approximation of the color brightness, shouldn’t it?
The problem is that some colors are brighter than others, red is brighter then blue and green is brighter then red, maybe we just need to find the right coefficients for them?
The W3C Algorithm
The W3C working draft on accessibility has a formula for the perceived brightness of a color (based on the YIQ color system):
((Red value X 299) + (Green value X 587) + (Blue value X 114)) / 1000
This formula and references to it dominate the search results, probably because the W3C has high search engine rank.
This is better than using HSL, but it tends to give wrong results for many colors, especially shades of yellow.
RGB Color Difference
The W3C also has an algorithm to calculate the difference between colors:
(maximum (Red value 1, Red value 2) - minimum (Red value 1, Red value 2)) + (maximum (Green value 1, Green value 2) - minimum (Green value 1, Green value 2)) + (maximum (Blue value 1, Blue value 2) - minimum (Blue value 1, Blue value 2))
Or, in shorter form:
dR + dG + dB
Where dR, dG and dB are the difference in the Red, Green and Blue component.
If you calculate difference from white and difference from black – and compare them (if difference from black>difference from white then the color is dark) you actually get better results than using the brightness formula, but then you get wrong results for light greens and dark blues (probably because this formula doesn’t take into account the brightness difference of the colors).
3D Distance in RGB Space
You can think of the RGB color space as a cube where each of the 3 colors are axis, in one corner you have black (RGB 0,0,0) and in the opposite corner you have white RGB (255,255,255), so if a color is closer to black it should be darker.
The formula for 3D distance is:
Sqrt(dx2+dy2+dz2)
Where dx, dy and dz are the difference on the x, y and z axis.
This algorithm also gives mixed results because it doesn’t take into account the fact that some colors look brighter than others - and that’s gets us back to …
Weighted Distance in 3D RGB Space (or the HSP algorithm)
If you scroll up to the beginning of this post and look at the brightness formula there you will see it’s just like the 3D distance formula except it gives different weight to each axis.
So now we finished our tour to color brightness land we have a good formula for calculating perceived brightness and (if my explanations where clear) we can actually understand why it works.
posted @ Sunday, April 27, 2008 6:30 PM